The alternate segment theorem is much easier to understand by looking at diagrams than by reading long definitions.
Most students struggle with this topic not because it’s hard—but because it’s often taught theory first, picture later. In this guide, we flip that approach.
Before learning any definition, you must recognize the shape.
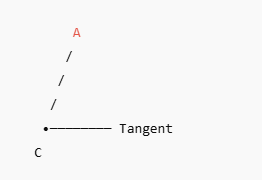
What you see here:
A circle
A tangent touching the circle at one point (C)
A chord (CA) from the same point
👉 If you see this setup, the alternate segment theorem applies.
Angle between tangent & chord
=
Angle inside the circle (opposite arc)
Diagram Showing the Rule
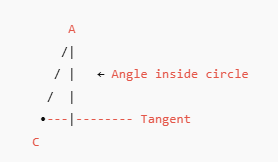
✔ The angle at C (tangent + chord)
✔ Equals the angle at A (inside the circle)
That’s the entire theorem.
Because the matching angle comes from the alternate (opposite) segment of the circle.
Visual Meaning
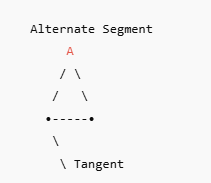
The angle is not near the tangent
It lies in the opposite segment of the circle
That’s where the name comes from.
Students should NOT memorize text.
They should follow visual steps.
Step 1: Is there a tangent?
Line touching circle once → Tangent ✔
Step 2: Is there a chord from the same point?
Yes → Theorem applies ✔
Step 3: Look inside the circle (opposite side)
That angle = tangent–chord angle ✔
There is no algebraic formula.
Instead, remember this angle relationship:
Angle between tangent and chord = angle in the opposite arc
This is how it appears in GCSE and IB exams.
This is important for IB and higher-mark GCSE questions.
Step 1 — Draw the Radius
✔ A radius is perpendicular to a tangent
✔ This gives a 90° angle
Step 2 — Use Circle Angle Rules
✔ Angles in the same segment are equal
✔ This links the tangent angle to the internal angle
✅ Proof complete
Example 1: One-Step Question
Given:
Angle between tangent and chord = 35°
Answer:
Angle inside circle = 35°
✔ By the alternate segment theorem
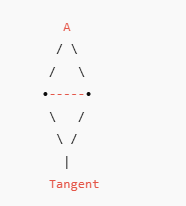
How to Solve:
Use alternate segment theorem to find one angle
Use triangle angle sum (180°) to find the rest
✔ This structure appears frequently in GCSE & IB exams
Most questions ask you to:
Find x
Calculate missing angles
Give reasons
Write a short proof
✔ Correct diagram
✔ Correct theorem name
✔ Clear reasoning
At GCSE level:
Diagrams are clear
Angles are usually integers
Proofs are short
“The angle between the tangent and chord equals the angle in the opposite arc.”
IB questions often include:
Multiple steps
Written reasoning
Links to other theorems
Especially common with cyclic quadrilaterals.
Apply alternate segment theorem
Then use:
Opposite angles in a cyclic quadrilateral = 180°
⭐ High-frequency IB exam combination
Line cutting through the circle (not a tangent) Using wrong internal angle Forgetting the chord must start at contact point
Correct Shape Reminder:
✔ Touch once
✔ Chord from same point
✔ Angle in opposite arc
Before applying the theorem:
Do I see a tangent?
Is there a chord at the same point?
Is the angle inside the opposite arc?
✔ Yes to all → Use the theorem
The angle between a tangent and a chord equals the angle inside the opposite part of the circle.
Yes, it is a core GCSE circle theorem.
By using the perpendicular radius rule and angles in the same segment.
No—only an angle relationship.
Yes, especially with cyclic quadrilaterals and proofs.
Using the theorem when there is no tangent.
IB Demystified is a trusted online learning platform led by certified IB examiners and educators.
© 2026 IB Demystified LTD
ALL RIGHTS RESERVED.
Powered by AfiaDigital