Understanding the integral of natural log of x, written as
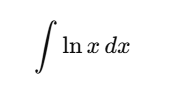
is a common challenge for students learning calculus. At first glance, it looks confusing because there is no direct integration formula for ln x.
But once you understand the idea behind the method, this integral becomes one of the easiest and most logical problems in calculus.
In this guide, you’ll learn:
Why this integral feels difficult
The exact method used to solve it
Step-by-step solutions
Variations of the question students search for
Common mistakes
Exam and IB-style tips
Real understanding, not memorization
The natural logarithm, written as ln x, is the logarithm with base e:
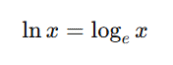
It appears frequently in:
Growth and decay problems
Integration and differentiation
Physics and economics
IB Math AA & AI syllabi
Before integrating ln x, remember one important fact:
ln x is NOT a simple power of x, so standard integration rules do not apply directly.
For most integrals, students use formulas like:
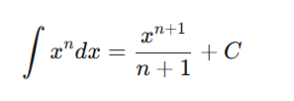
But ln x does not match any standard integration rule.
That’s why we use a powerful technique called:
The formula for integration by parts is:
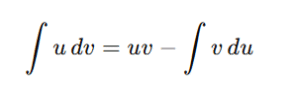
This method is used when:
A function cannot be integrated directly
The integrand is a product (or can be turned into one)
Even though ln x looks like a single function, we cleverly rewrite it as:
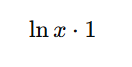
This allows us to apply integration by parts.
For
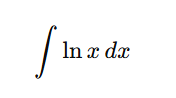

Start with:
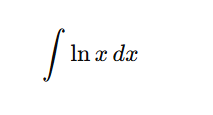
Apply integration by parts:
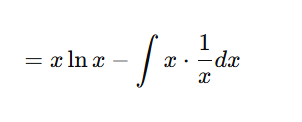
Simplify:
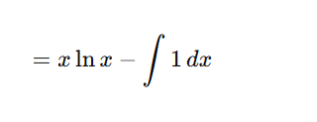
Integrate:
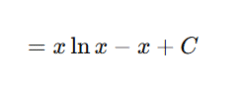
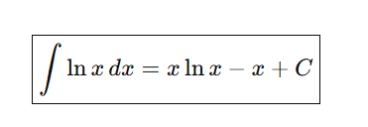
This is the standard result and must be memorized after understanding, not before.
The x ln x term comes from multiplying ln x by x
The −x corrects the overestimation caused by that multiplication
The constant C accounts for infinite antiderivatives
This balance is exactly what integration by parts achieves.
❌ Trying to integrate ln x directly
❌ Forgetting the minus sign
❌ Forgetting the constant of integration
❌ Wrong choice of u and dv
❌ Writing ln x as 1/x (confusing with derivative)
👉 Remember:
Derivative of ln x = 1/x
Integral of ln x ≠ 1/x
These variations appear frequently in exams and homework:
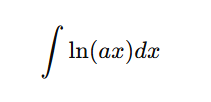
Use log laws:
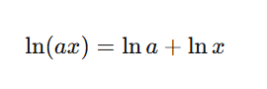
Solution:
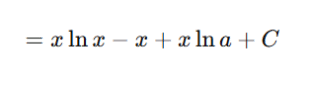
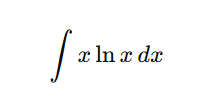
Use integration by parts again:
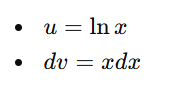
Final answer:
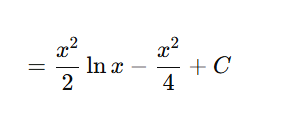
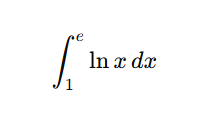
Use:
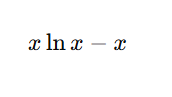
Evaluate:
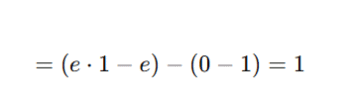
ln x grows slowly
The area under ln x increases steadily
The negative region (x < 1) matters in definite integrals
👉 Including a sketch of y = ln x earns method marks in exams.
Always state integration by parts
Show u, du, v, dv clearly
Add a short explanation (earns communication marks)
Include units if in applied context
For IAs, connect ln x integrals to:
Growth models
Logarithmic scales
Natural decay
Exponential growth & decay
Entropy in physics
Economics (log utility models)
Population modeling
Signal processing
Understanding this integral builds conceptual strength, not just exam success.
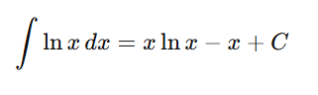
Method:
Use integration by parts
Choose u = ln x
Choose dv = dx
Because ln x cannot be integrated directly using standard rules.
Yes, in IB Math AA and AI, especially in calculus units and exams.
No. Integration by parts is the standard and expected method.
Confusing the derivative of ln x with its integral.
Understand first, then memorize — that’s how exam confidence is built.

IB Demystified is a trusted online learning platform led by certified IB examiners and educators.
© 2026 IB Demystified LTD
ALL RIGHTS RESERVED.
Powered by AfiaDigital
WhatsApp us