
Every student, at some point, wishes maths could be just a little easier. When exams get close, formulas start to look like a huge wall blocking your success. That’s exactly why a maths formula sheet is so important — it turns that wall into a clear, simple path.
A well-organized maths formula sheet is more than a list of formulas. It’s a cheat-code for understanding, revising, and performing better in your exams. Whether you’re in IB, IGCSE, GCSE, or any other system, these formulas are the backbone of your maths preparation.
Math anxiety is real — students often feel:
• “There’s too much to memorize.”
• “I study for hours but still forget formulas.”
• “I know the formula… but I don’t know where to use it.”
• “Exams make my mind blank.”
A clear maths formula sheet solves this by helping you:
✔ Revise faster
✔ Understand where each formula applies
✔ Boost confidence
✔ Reduce silly mistakes
✔ Strengthen exam memory
✔ Save time during revision
1. (a + b)² = a² + 2ab + b²
Example:
(5 + 2)² = 25 + 20 + 4 = 49
2. (a – b)² = a² – 2ab + b²
Example:
(6 – 1)² = 36 – 12 + 1 = 25
3. a² – b² = (a + b)(a – b)
Example:
9 – 4 = (3 + 2)(3 – 2) = 5 × 1 = 5
a³ + b³ = (a + b)(a² – ab + b²)
a³ – b³ = (a – b)(a² + ab + b²)
Example:
Factorize 64 – 27
→ 4³ – 3³
= (4 – 3)(16 + 12 + 9) = 1 × 37 = 37
ax + b = 0
x = –b/a
Example:
9x + 18 = 0 → x = –2
• Triangle = ½ × base × height
• Square = side²
• Rectangle = l × w
• Circle = πr²
Example:
Area of triangle (base 10, height 8)
→ ½ × 10 × 8 = 40
• Square = 4 × side
• Rectangle = 2(l + w)
• Circle circumference = 2πr
Example:
Circle with radius 4
→ 2 × 3.14 × 4 = 25.12
a² + b² = c²
Example:
Legs = 9, 12
c = √(81 + 144) = √225 = 15
sinθ = opposite/hypotenuse
cosθ = adjacent/hypotenuse
tanθ = opposite/adjacent
sin²θ + cos²θ = 1
tanθ = sinθ/cosθ
cotθ = 1/tanθ
secθ = 1/cosθ
cosecθ = 1/sinθ
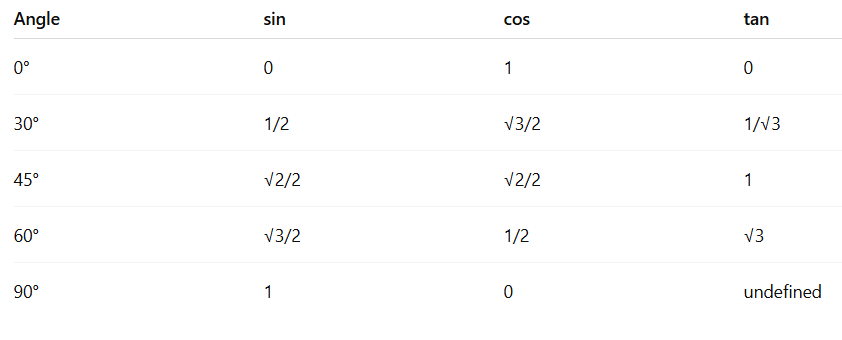
If sinθ = 4/5, find cosθ.
→ cos²θ = 1 – 16/25 = 9/25
→ cosθ = 3/5
• Cube = 6a²
• Cuboid = 2(lb + bh + hl)
• Sphere = 4πr²
• Cylinder = 2πrh + 2πr²
• Cube = a³
• Cuboid = l × b × h
• Cylinder = πr²h
• Sphere = 4/3 πr³
Example:
Volume of a cylinder (r=3, h=10)
→ 3.14 × 9 × 10 = 282.6
d/dx (xⁿ) = nxⁿ⁻¹
d/dx (sin x) = cos x
d/dx (cos x) = –sin x
d/dx (eˣ) = eˣ
d/dx (ln x) = 1/x
Example:
d/dx (x⁴) = 4x³
∫ xⁿ dx = xⁿ⁺¹ / (n+1)
∫ sin x dx = –cos x
∫ cos x dx = sin x
∫ eˣ dx = eˣ
Example:
∫ x² dx = x³/3 + C
Distance = √[(x₂ – x₁)² + (y₂ – y₁)²]
Example:
Between (1,1) and (4,5)
→ √[(3)² + (4)²] = √25 = 5
Midpoint = ((x₁ + x₂)/2 , (y₁ + y₂)/2)
Slope = (y₂ – y₁) / (x₂ – x₁)
Mean = sum/n
Median = middle value
Mode = most common value
Example:
Data: 3, 5, 5, 8
Mean = (3+5+5+8)/4 = 21/4 = 5.25
P(E) = favorable outcomes / total outcomes
Example:
Probability of drawing an Ace from a deck
→ 4/52 = 1/13
Students often fear formulas, but here’s how to make them stick:
✔ Understand, don’t memorize
✔ Practice at least 3 questions per formula
✔ Use flashcards
✔ Keep a daily revision sheet
✔ Teach someone else
✔ Solve past papers
Memorizing formulas becomes effortless when you understand why they work.
Book an appointment with one of our top IB consultants or examiners. If you’re facing any challenges or have questions, simply reach out — our team will get in touch to discuss your needs. Together, we’ll decide the best time for a personalized 1-on-1 Zoom session designed to guide you every step of the way.

IB Demystified is a trusted online learning platform led by certified IB examiners and educators.
© 2026 IB Demystified LTD
ALL RIGHTS RESERVED.
Powered by AfiaDigital
WhatsApp us